冷轧板形目标曲线设定模型的研究与应用

来源：王鹏飞，张殿华，刘佳伟，王军生，俞小峰 |浏览：次|评论：0条 [收藏] [评论]

冷轧板形目标曲线设定模型的研究与应用

王鹏飞¹，张殿华，刘佳伟¹，王军生²，俞小峰²

(1．东北大学轧制技术及连轧自动化国家重点实验室，辽宁沈阳110004；2．鞍钢股份有限公司，辽宁鞍山114001)

摘要：为了提高冷轧带钢的板形质量，在1250单机架6辊可逆冷轧机的板形控制系统改造中，根据带材失稳模型判据制订了基本板形目标曲线模型。为了消除了生产中温度、卷形和设备安装误差等对板形测量的不利影响，根据设备运行情况以及轧制工艺制订了一系列补偿曲线。设定了手动调节板形的附加曲线，提高了实际生产中板形控制的灵活性。板形目标曲线设定模型投入使用后，经现场应用表明，在控制带钢凸度的同时保证了板形的控制效果，满足了后续工序对带钢凸度及板形的要求。冷轧带钢成品具有较高的板形精度，完全满足高精度板形控制的要求。

关键词：板形；目标曲线；补偿曲线；板凸度；平直度；冷轧

板形标准曲线模型是板形控制的基本模型之一，是板形控制的目标模型，目前国内引进的先进板形控制系统，只有一些可供选择的板形标准曲线，而没有制定板形标准曲线的原理、模型和方法，这是技术的源头和秘密，难以引进。在实际生产中如何选择板形标准曲线，也只有根据大量的操作经验，逐步摸索，属经验性选择，缺少理论分析计算，这对于轧制新产品是很不利的^[1]。本文通过理论计算结合实际冷轧生产中对板形控制的要求，建立了具体的板形目标曲线模型，并将其用于某冷轧厂1250单机架6辊可逆冷轧机的板形控制系统改造中，提高了板形控制的精度，实现了轧机对冷轧带钢的高精度板形控制。

1 板形目标曲线的设定方法

当来料和其它轧制条件一定时，一定形式的板形目标曲线不但对应着一定的板形，而且对应着一定的板凸度。选用不同的板形目标曲线，将会得到不同的板形和板凸度^[2]。通常，前几个道次带材较厚，不易出现轧后翘曲变形，且此时带材在辊缝中横向流动现象相对明显，因此充分利用这一工艺特点，选用合适的板形目标曲线，既可达到控制板凸度的目的，又不会产生明显的板形缺陷。此外，板形目标曲线还可以用来保持中间道次的比例凸度一致。

在1250单机架可逆冷轧机的板形控制系统改造中，根据轧制工艺及后续工序对带钢板形的要求，板形目标曲线的制定方案是：给定来料板凸度，前3个道次以轧后带材不失稳为限制条件，即以保证轧后带钢不发生翘曲为前提条件，尽量减小板凸度，后2个道次集中控制板形，使成品带钢尽可能具有较好的板形。

板形目标曲线是由各种补偿曲线叠加到基本板形目标曲线上形成的。基本板形目标曲线根据后续工序对带钢凸度的要求由过程计算机计算得到，然后传送给板形计算机。带钢凸度改变量的计算以带钢不发生屈曲失稳为条件，保证在对板凸度控制的同时，不会产生轧后瓢曲现象。补偿曲线主要是为了消除板形辊表面轴向温度分布不均匀、带钢横向温度分布不均匀、板形辊挠曲变形、板形辊或卷取机几何安装误差、带卷外廓形状变化等因素对板形测量的影响^[3]。与基本板形目标曲线不同，补偿曲线在板形计算机中完成设定。

1．1基本板形目标曲线

基本板形目标曲线主要基于对板凸度的控制设定。在减小带钢凸度时，为了不造成轧后带钢发生瓢曲，需要以轧后带材失稳判别模型为依据，不能一味地减小带钢凸度，必须保证板形良好。根据残余应力的横向分布，判别带材是否失稳或板形良好程度，从而决定如何进一步调整板凸度和板形。带材失稳判别模型是一个力学判据，机理是轧制残余应力沿板宽方向分布不均匀而发生屈曲失稳的结果^[4]。

轧后带材失稳判别模型基于带钢的屈曲理论来制定，计算方法主要有：解析法、有限元法、有限条法和条元法^[1]。本文采用条元法进行板形良好判据的计算。条元法用一个判别因子ξ判断板形状况^[5-6]，即：

式中，ξ为带钢失稳判别因子。

基本板形目标曲线的设定以轧后带材失稳判别模型为依据，充分考虑来料带材凸度以及后续工序对带钢板形的要求。基本板形目标曲线的形式为二次抛物线，由过程计算机计算抛物线的幅值，并传送给板形计算机。基本板形目标曲线的形式为：

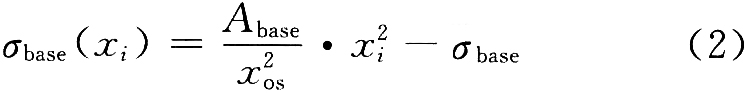
式中σ_base(x_i)为每个测量段处带钢张应力偏差的设定值；A_base为过程计算机依据带钢板凸度的调整量以及带材失稳判别模型计算得到的基本板形目标曲线幅值，单位是N／m²，其符号与来料形貌有关；x_i为以带钢中心为坐标原点的各个测量段的坐标，带符号，操作侧为负，传动侧为正；x_os为操作侧带钢边部有效测量点的坐标；为平均张应力。

过程计算机计算幅值A_base时，根据不同的来料带钢规格，以带材失稳判别模型为基础，在保证板形不产生缺陷，即判别因子ξ>1的情况下，在前几道次尽可能地减小带钢凸度。在后几道次则着重控制板形，保持带钢比例凸度一致。

平均张应力计算公式为：

式中，n为板形有效测量段数。

在1250冷轧机的板形控制系统中，板形辊共有23个测量段，因此带钢上最大有效测量段数为23。基本板形目标曲线的形式为二次曲线，在每个道次开始时，板形计算机接收到过程计算机发送的幅值后，首先判断带钢是否产生跑偏，然后根据传动侧和操作侧的带钢边部有效测量点来确定总的有效测量点数，并按照式(2)逐段计算每个有效测量点处的张应力设定值，最终形成完整的板形目标曲线，如图1所示。

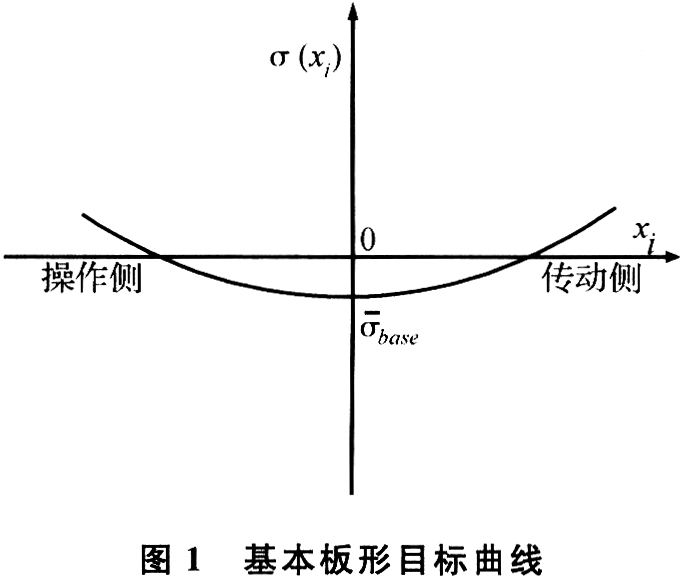
其次，由带材内应力自相平衡条件，在带钢宽度范围内，基本板形目标曲线还应满足下式：

1．2卷取形状补偿

卷形修正又称为卷形补偿，由于带钢横向厚度分布呈正凸度形状，随着轧制的进行，卷取机上钢卷卷径逐渐增大，致使卷取机上钢卷外廓沿轴向呈凸形或卷取半径沿轴向不等，这将导致带钢在卷取时沿横向产生速度差，使带钢在绕卷时沿宽度方向存在附加应力。卷取附加应力的计算公式为：

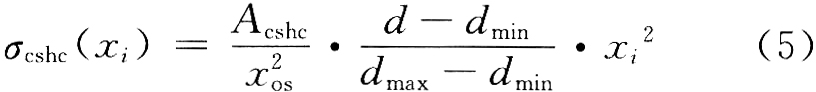
式中：A_cshc为卷形修正系数，N／m²，由过程计算机根据实际生产工艺计算得到；d为当前卷取机卷径；d_min为最小卷径；d_max为最大卷径。

1．3卷取机安装几何误差补偿

由于设备安装条件限制，常常会出现卷取机轴线与板形辊轴线不平行的情况。由于卷取过程中存在不均匀的卷取张力，这必然会对带钢的板形测量造成影响，如图2所示。

为了消除这种影响，在板形目标曲线中增加了卷取机安装几何误差补偿环节，该误差补偿为线性修正，根据卷取机与板形辊之间的偏斜方向及偏斜角度来制定，其计算公式为：

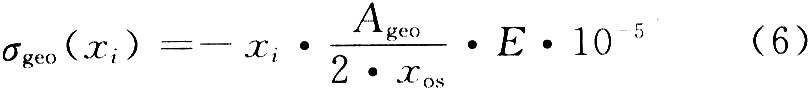
式中：A_geo为线性补偿系数，I；E为弹性模量。

A_geo的单位为I，是一个板形值，与卷取机及板

形辊轴线之间的偏斜方向和偏斜角度有关，表征了由于卷取机轴线与板形辊轴线之间的偏斜，导致的板形辊操作侧与传动侧之间产生的板形偏差大小。当卷取机传动侧在水平方向低于操作侧时，A_geo值为负，反之为正。

1．4带钢横向温差补偿

轧制过程中，变形使带钢在宽度方向上的温度存在差异，它将引起带钢沿横向出现不均匀的横向热延伸，这反映为卷取张力沿横向产生不均匀的温度附加应力^[7]。如不修正其影响，尽管在轧制过程中将带钢应力偏差调整到0，仍不能获得具有良好平直度的带钢。这是因为当带钢横向温差较大时，板形辊在线实测板形与轧后最终实际板形并不相同，轧后带钢温差消失后，沿带钢横向原来温度较高的部分由于热胀冷缩的影响会产生回缩，从而影响板形控制效果^[8]。当带钢横向两点之问存在Δt(℃)的温差时，按照线弹性膨胀简化计算，则可以得到产生的浪形为^[9]：

式中：Δl、l分别为带钢长度方向上的延伸差和基准长度；α为带钢热膨胀系数，取1．17×10^-5。

该1250冷连轧机分为5道次轧制，在经过前几个道次的轧制后，带钢产生了较大的变形量，导致带钢在宽度上有较大的温差，必将影响最终的板形控制效果。为了消除带钢横向温差对轧后板形的影响，可以采用设定温度补偿曲线的方法。

由式(7)结合胡克定律可知温度附加应力表达式为：

Δσ_t(x)=k·t(x) (8)

式中：Δσ_t (x)为不均匀温度附加应力；k为比例系数，取2．5；t(x)为温差分布函数。

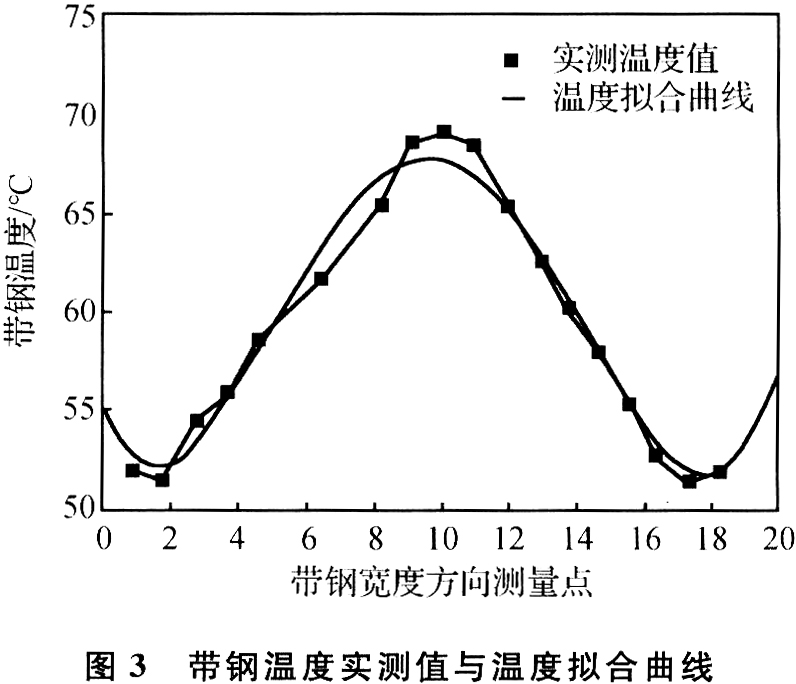
使用红外测温仪实测出末机架出口带钢各部位温度后，通过曲线拟合可以确定其温度分布函数，如图3所示。经过数学处理后的温差分布函数为：

t(x)=ax⁴ bx³ cx² dx m (9)

式中：a、b、c、d、m为曲线拟合后的温差分布函数的系数；z为带钢宽度方向坐标。

则用于抵消带钢横向温差产生的附加应力曲线为：

σ_t (x_i)=一2．5(ax_i⁴ bx_i³ cx_i² dx_i m) (10)

1．5边部减薄补偿

冷轧带钢的横截面轮廓形状，除边部区域外，中间区域的带钢断面大致具有二次曲线的特征。而在接近边部处，厚度突然迅速减小，形成边部减薄，就是生产中所说的边缘降，简称边降^[10]。边部减薄是带钢重要的断面质量指标，直接影响到边部切损的大小，与成材率有密切的关系。为了降低边部减薄，制定了边部减薄补偿方案，根据生产中边部减薄的情况，在操作侧和传动侧各选择若干个测量点进行补偿，操作侧补偿计算公式为：

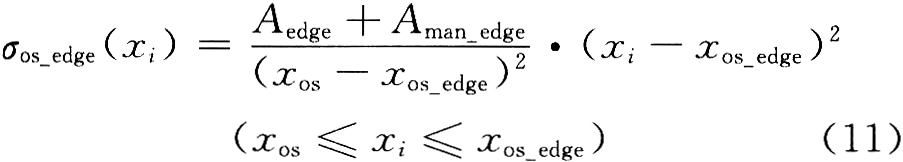
式中：A_edge妇为边部减薄补偿系数，根据生产中出现的带钢边部减薄情况确定，由过程计算机计算得到，发送给板形计算机；A_{man_edge}为边部减薄系数的手动调节量，这是为了应对生产中边部减薄不断产生变化而设定的，由斜坡函数生成，并经过限幅处理；x_{os_edge}为从操作侧第一个有效测量点起，最后一个带有边部减薄补偿的测量点坐标，它们都是整数。

则操作侧进行边部减薄补偿的测量点个数为：

n_os=∣x_os- x_{os_edge}∣ (12)

传动侧的边部减薄补偿计算公式为：

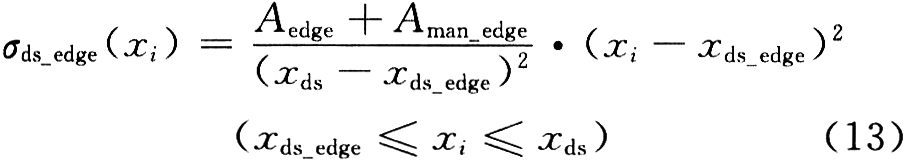
式中：x_{ds_edge}为从传作侧第一个有效测量点起，最后一个带有边部减薄补偿的测量点坐标。

操作侧进行边部减薄补偿的测量点个数为：

n_ds=∣x_ds- x_{ds_edge}∣ (14)

根据轧制工艺及生产中出现的边部减薄情况，一般将操作侧和传动侧边部补偿的测量点数目相同，即n_os=n_ds。

1．6板形调节机构的手动调节附加曲线

为了得到更好的板形控制效果，以及更适应实际生产的灵活性，除了补偿各种影响因素对板形测量造成的影响，还根据轧机具有的板形调节机构对板形控制的特性，分别制定了弯辊和轧辊倾斜手动调节附加曲线，可以根据实际生产中出现的板形问题，由操作工在画面上在线调节板形目标曲线。

1)弯辊手动调节附加曲线：

σ_bend(x_i)= A_{man_bend}·x_i²/x_os² (15)

式中：A_{man_bend}为弯辊手动调节系数，不进行手动调节时值为0，调节时由斜坡函数生成，并经过限幅处理。

2)倾斜手动调节附加曲线：

σ_tilt(x_i)= A_{man_tilt}·x_i/(2·x_os) (16)

式中：A_{man_tilt}为轧辊倾斜手动调节系数，不进行手动调节时值为0，调节时由斜坡函数生成，并经过限幅处理。

2 板形目标曲线设定模型的实际应用

实际用于板形控制的板形目标曲线是在基本板形目标曲线的基础上叠加补偿曲线和手动调节曲线形成的。具体方法是：首先计算各个有效测量点的补偿量及手动调节量的平均值，然后将各个测量点的补偿设定值减去该平均值得到板形偏差量，将板形偏差量叠加到基本目标板形曲线上即可得到板形目标曲线。各个有效测量点补偿量及手动调节量的平均值为：

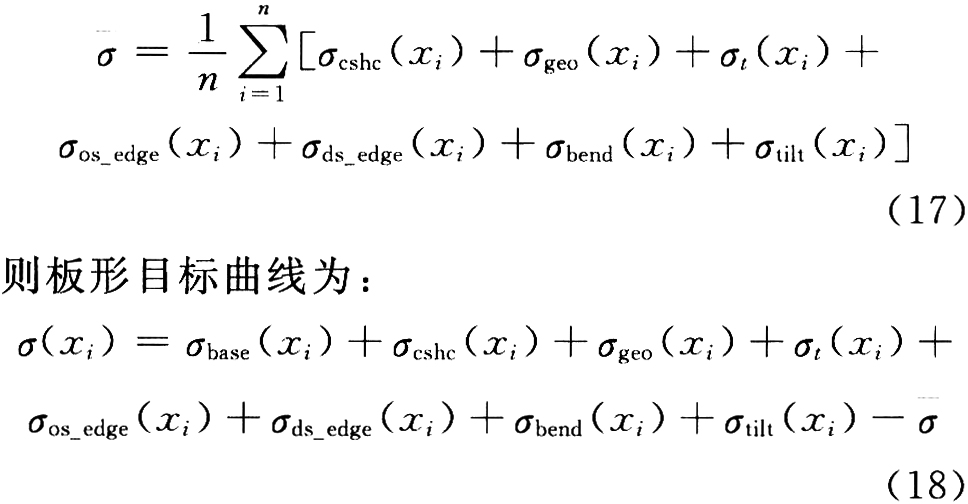
2．1板形目标曲线模型在板形控制系统中的实际应用

在板形控制系统中，为了简化数据处理过程，将实际板形测量点沿宽度方向插值为若干个特征点，如图4所示，然后计算每个特征点处的张应力设定值，作为板形控制的张应力分布的目标偏差值。图4中数轴X₁为板宽方向的实际有效测量点分布，每个测量点处对应一个目标张应力σ_t(x_i)，数轴X₂为板宽方向的特征点分布，每个特征点处对应一个经过差值计算的目标张应力σ_t，这些特征点处的目标张应力将作为板形目标偏差用于板形闭环反馈控制系统中。

将数轴X₂上每个特征点i对应于数轴X₁上的一个坐标x，由数轴X₂上的特征点i转化为数轴X₁上的一个坐标z的计算方法如下：

x=(n₁-1)·i/(n₂-1) (19)

式中，n₁、n₂分别为板宽方向的有效测量段(点)数和特征点数。

得到数轴X₂上的特征点在数轴X₁上对应的坐标x后，首先确定该坐标在数轴X₁上的2个边界点x_i-1和x_i，再利用这2个边界点处的目标张应力插值计算坐标x处的目标张应力，计算方法如下：

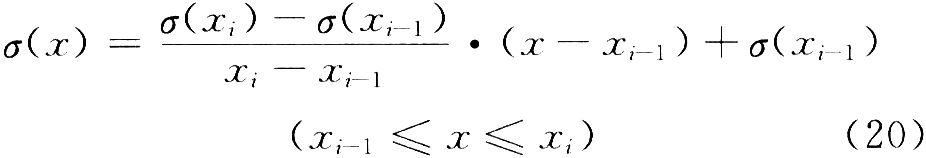
则数轴X₂上的特征点i处的目标张应力为：

σ_i=σ（x） (21)

数轴X₂两端处的特征点不需要进行处理，只是取数轴X₁上操作侧和传动侧边部第一个有效测量点处的目标张应力值，即σ₀=σ(x₀)，σ_n2-1=σ(x_n1-1)

在1250单机架可逆冷轧机的板形控制系统改造中，板形辊有23个测量段，板宽方向的特征点设定为20个。使用上述计算方法确定处理后的板形目标曲线后，将其用于板形闭环反馈控制系统中。板形闭环反馈控制采用的计算模型是基于最小二乘评价函数的板形控制策略。它以板形调控功效为基础，使用各板形调节机构的调控功效系数及板形辊各测量段实测板形值运用线性最小二乘原理建立板形控制效果评价函数，求解各板形调节机构的最优调节量。评价函数为：

式中：J为评价函数；”为板宽方向特征点数；g_i为板宽方向上各特征点的权重因子，代表调节机构对板宽方向各个特征点处的板形影响程度，边部特征点的权重因子要比中部区域大；σʹ_i为第i个特征点处板形实测值，同板形目标曲线一样，经过由板宽方向的测量段到特征点的处理；m为板形调节机构数目，△u_j为第歹个板形调节机构的调节量，E_ff_，ij为第j个板形调节机构对第i个测量段的板形调节功效系数。

使J最小时有：

∂J/∂Δu_j=0 (j=1，2，…，m) (23)

可得仇个方程，求解方程组可得各板形调节结构的调节量△u_j。

板形调控功效由自学习过程确定。板形控制系统首先根据板形偏差计算出轧辊的倾斜量，然后从板形偏差中减去轧辊倾斜所调节的板形偏差，再从剩余的板形偏差中计算工作辊的弯辊量，按照这种接力方式依次计算出中间辊正弯辊量、中间辊横移量。计算出的板形调节机构调节量需要经过限幅，变增益补偿环节的处理，再输出给各板形调节机构控制器。最后残余的板形偏差由分段冷却消除。调节机构的执行顺序会影响板形控制效果，需要按照各调节机构的特性以及设备状况制定执行顺序：各板形调节机构之间具有替代模式，当计算出的某个调节机构的调节量超限时，则使用另外一个调节机构来完成超限部分调节量。

2．2模型应用效果

本模型已用于某1250单机架6辊可逆冷轧机改造项目中，板形测量装置采用的是国产无辊环式板形辊：辊径350mm，测量段数目23个，辊身长度1 350mm，测量段宽度52mm。为了检测模型的使用效果，从PDA中引出相应的在线实测数据进行分析。

表1为模型投入后2个冷轧卷带钢凸度的变化情况，来料规格分别为：2．62 mm×1 020 mm、2．76mm×1 053mm。由表1中数据可知，轧制具有中凸断面的带钢时，2卷带钢的凸度分别从来料的28．4μm和29．7μm逐步减少到5．23μm和5．62μm。前3个道次凸度消除的较多，轧后带钢凸度分布均匀，满足了下游工序对带钢板形的要求。

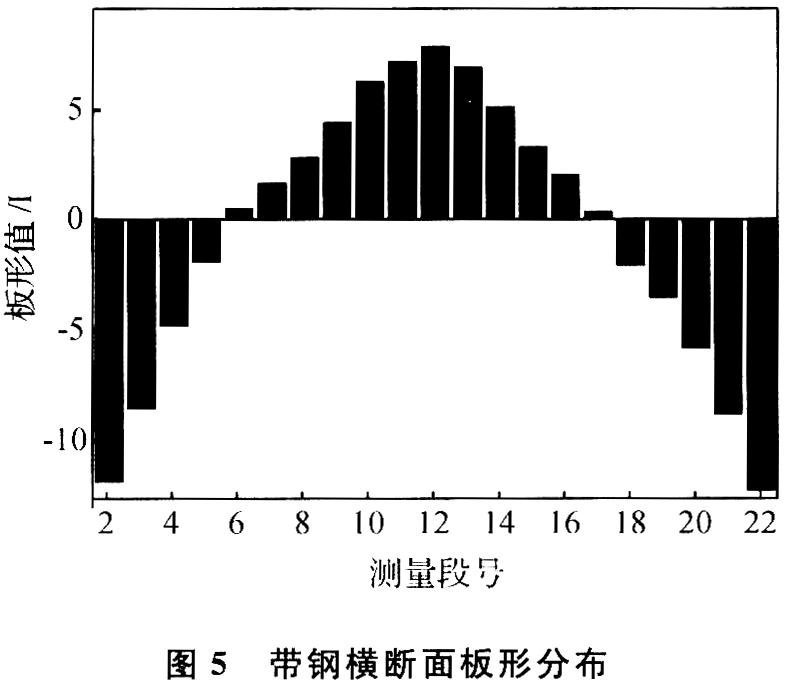
在减小带钢凸度的同时，带钢板形也取得了很好的板形控制效果。图5为模型投入后，末道次带钢的一组沿带钢宽度方向上的板形测量值分布图，产品规格(厚×宽)：0．8 mm×1 090 mm，材质为STl2，轧制速度500～600m／min。由数据分析可知，带钢横断面板形偏差基本上控制在10 I以内。同时，边部减薄情况也得到了明显的减轻，相比模型投入前，边部减薄可以控制在5μm以内。加曲线，提高了实际生产中板形控制的灵活性。

3)板形目标曲线设定模型投入使用后，经现场应用表明，冷轧带钢产品具有较高的板形精度，完全满足高精度板形控制的要求，为冷轧板形控制提供了新的思路。

3 结论

1)根据板材屈曲理论建立了带材失稳模型判据，并据此判据制订了基本板形目标曲线模型，在减小冷轧带钢凸度的同时保证了板形的控制效果，满足了后续工序对带钢凸度及板形的要求。

2)分析了影响板形测量的因素，针对设备运行情况以及轧制工艺制订了一系列补偿曲线，消除了生产中温度、卷形和设备安装误差等对板形测量的不利影响。设定了带钢边部减薄补偿曲线，有效地控制了带钢的边部减薄。设定了手动调节板形的附加曲线，提高了实际生产中板形控制的灵活性。

参考文献

[1]刘宏民，丁开荣，李兴东，等．板形标准曲线的理论计算方法[J]．机械工程学报，2008，44(8)：138．

[2]连家创，刘宏民．板厚板形控制[M]．北京：兵器工业出版社，1996．

[3]贾生晖，张杰，曹建国，等．冷连轧机硅钢板形控制目标的改进[J]．北京科技大学学报，2002，24(3)：303．

[4]杨荃，陈先霖．冷轧机的板形控制目标模型[J]．北京科技大学学报，1995，17(3)：255．

[5] Liu Hongmirl，Peng Yan，Chu Yupeng，et a1．Strip Element Method for Shape Discrimination 0f St rip rolling[J]．Communictions in Numerical Methods in Engineering，2004,20（9）：709

[6]刘宏民，彭艳，褚宇鹏．板带轧制板形判别的条元法[J]．燕山大学学报，2002，26(2)：95．

[7]贾春玉，尚志东．冷轧板形目标曲线的补偿设定[J]．钢铁研究学报，2000，12(4)：65．

[8] Ruben Usamentiaga，Daniel F．Garcia．Compensation for Uneven Temperature in F1atness Contro1 Systems for Steel Strips[J]．conference Record of the 2006 IEEE，2006，l：521．